이전 Chapter에서는 ray 객체를 정의하고 Project Space에 대한 Vector들을 통해 ray_color라는 함수를 이용하여 Pixel의 색상을 결정해보았다.
이번 Chapter에서는 하나의 Object를 추가해보자. 일반적으로는 Ray Tracer에 Sphere (구체)를 많이 이용하는데, 이는 ray가 구체에 닿았을때에 대한 계산이 상당히 직관적이어서 그렇다.
1. Ray-Sphere Intersection
우리는 학교에서 기하학을 배웠다면 구의 방정식을 알고 있을 것이다. 구의 중심점으로부터 반지름을 이라고 했을 때, 가 구의 방정식이다.
구의 방정식을 통해서 특정 점이 구의 안에 있는지, 밖에 있는지, 걸쳐 있는지 알 수 있다. 만일 좌표가 구 위에 걸쳐 있다면, 가 된다. 또한 주어진 좌표 좌표가 구 안에 존재한다면, 가 됨을 알 수 있고, 구의 밖에 존재한다면 임을 알 수 있다.
일반적으로 주어지는 는 구의 중심점이 에 해당할 때의 방정식이다. 따라서 구의 중심점이 라고 한다면, 구의 방정식은 다음과 같이 나타난다.
Graphics에서는 이러한 공식들을 대체적으로 Vector의 형태로 나타나기 때문에 공식에서 주어진 , , 에 대한 식들은 vec3 Class로 나타낼 수 있다. 예를들어 중심점 는 로, 점 는 로 표현할 때 주어진 두 점에 대한 Vector는 가 된다. 주어진 Vector를 구의 방정식 형태로 나타내기 위해서 에 를 Dot Product하면 다음과 같이 나타난다.
이 였으므로 역시 이 된다.
구의 방정식을 Vector로 표현 했기 때문에 우리는 구체 위의 임의의 점을 라고 했을 때 ray가 구체에 닿는지 확인을 하는 것이 가능하다. 이 때 ray는 저번 Chapter에서 다뤘던 식처럼 시작점 에 대해 방향 와 Parameter 를 이용하여 인 로 표현할 수 있었다. 만일 ray가 구체에 닿는다면, 는 구의 방정식을 만족할 것이다. (즉, 구의 방정식을 만족한다는 말은 가 구체 위의 임의의 점인 를 만족하는 것이다.) 따라서 다음과 같은 공식이 성립한다.
위 식을 ray를 구하는 형태로 바꿔보면 이 되는데 이를 Vector Algebra의 규칙을 만족시키기 위해 펼쳐놓은 방정식을 좌항으로 모두 옮겨서 표현하면 다음과 같이 나온다.
는 Vector이고, 는 Parameter이다.
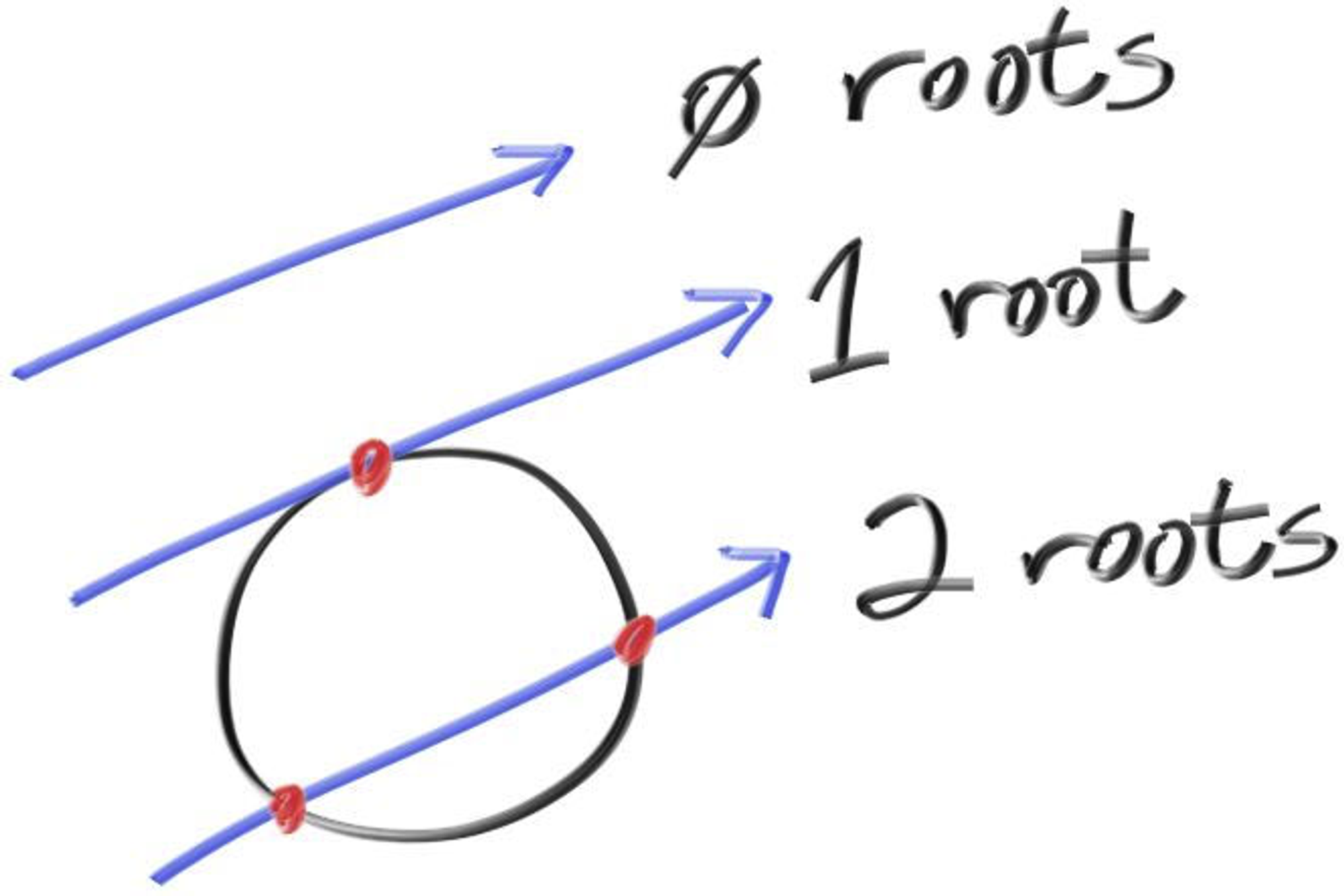
주어진 식에서 를 제외한 모든 값들은 상수로 정해져 있는 2차 방정식의 형태이므로 에 대해서 풀어낼 수 있다. 근의 공식 중에 판별식 를 통해서 근의 개수를 알아낼 수 있는데, 판별식 가 양수라면 근이 2개, 음수라면 근이 0개, 이라면 근이 1개이다. 구해낸 근의 개수는 Graphics에서 기하학적으로 접근할 수 있다. 아래 그림과 같은 해석이 가능하다.
2. Creating Our First Raytraced Image
이전에 Vector Algebra에 따라서 풀어낸 식을 이용하여 코드를 작성하면 된다. 아래의 코드를 main.cpp에 추가하고, ray_color 함수를 수정한다.
#include "vec3.h"
#include "color.h"
#include "ray.h"
bool hit_sphere(const point3& center, double radius, const ray& r)
{
vec3 oc = r.origin() - center;
auto a = dot(r.direction(), r.direction());
auto b = 2.0 * dot(oc, r.direction());
auto c = dot(oc, oc) - radius * radius;
auto discriminant = b * b - 4 * a * c;
return (discriminant > 0);
}
color ray_color(const ray& r)
{
if (hit_sphere(point3(0, 0, -1), 0.5, r))
return (color(1, 0, 0));
vec3 unit_direction = unit_vector(r.direction());
auto t = 0.5 * (unit_direction.y() + 1.0);
return (1.0 - t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}
int main(void)
{
// Image
const auto aspect_ratio = 16.0 / 9.0;
const int image_width = 400;
const int image_height = static_cast<int>(image_width / aspect_ratio);
// Camera
auto viewport_height = 2.0;
auto viewport_width = aspect_ratio * viewport_height;
auto focal_length = 1.0;
auto origin = point3(0, 0, 0);
auto horizontal = vec3(viewport_width, 0, 0);
auto vertical = vec3(0, viewport_height, 0);
auto lower_left_corner = origin - horizontal / 2 - vertical / 2 - vec3(0, 0, focal_length);
// Render
std::cout << "P3\n" << image_width << ' ' << image_height << "\n255\n";
for (int j = image_height - 1; j >= 0; --j)
{
std::cerr << "\rScanlines Remaining: " << j << ' ' << std::flush;
for (int i = 0; i < image_width; ++i)
{
auto u = double(i) / (image_width - 1);
auto v = double(j) / (image_height - 1);
ray r(origin, lower_left_corner + u * horizontal + v * vertical - origin);
color pixel_color = ray_color(r);
write_color(std::cout, pixel_color);
}
}
std::cerr << "\nDone.\n";
return (0);
}
C++
복사
작성한 코드를 실행하면 자그마한 구체에 빛이 맞는 부분은 빨간색으로 나타나게 된다. (구체는 축의 Focal Length에 따라 에 위치해 있다고 가정한다.) 따라서 아래 그림과 같은 형태를 얻을 수 있다.
비록 정말 많이 부족한 형태의 구체이지만 (쉐이딩, 빛의 반사, 여러 Object에 대한 적용 등...) 굉장히 성공적으로 물체를 그래픽으로 담아냈다. ray가 구체에 닿는지 판별하는데 있어서 ray를 쏘는 방향의 Parameter인 값이 양수 (즉, 화면 안에 존재한다)라는 가정하에 진행한 것인데, 구체에 닿는 판별식 자체가 2차 방정식으로 풀어내기 때문에 값이 음수 (즉, 화면 밖에 존재한다)라고 해도 동일한 판별식으로 처리되는 문제가 있다. 물론 값이 음수라는 말은 ray를 뒷 방향으로 쏘았기 때문에 구체가 기존처럼 축의 이 아닌 에 위치한 것으로 정정하여 정상적인 작동을 확인할 수 있다. 여튼 카메라 뒤에 있는 물체에 대해서 카메라 앞에 있는 것과 동일한 상이 잡히는 문제에 대해서는 차후에 해결하니 걱정하지 않아도 된다.