1. 들어가기 전에
실수를 표현하는 방법은 고정 소수점 방식과 부동 소수점 방식, 총 2가지 방법이 있다. 정확도 자체는 고정 소수점 방식이 높지만 대부분의 컴퓨터는 부동 소수점 방식을 이용한다. 이유가 있을까? 고정 소수점 방식의 경우 소수점에 이용하는 범위를 딱 고정을 해놓기 때문에 수의 표현 범위가 크지 않다. 반면에 부동 소수점 방식은 소수점을 이용하지 않으면 그만큼 다른 수를 표현할 수 있도록 더 넓은 표현 범위를 갖는다. 이 때문에 고정 소수점 방식보다 부동 소수점 방식을 더 많이 이용하는 것이다.
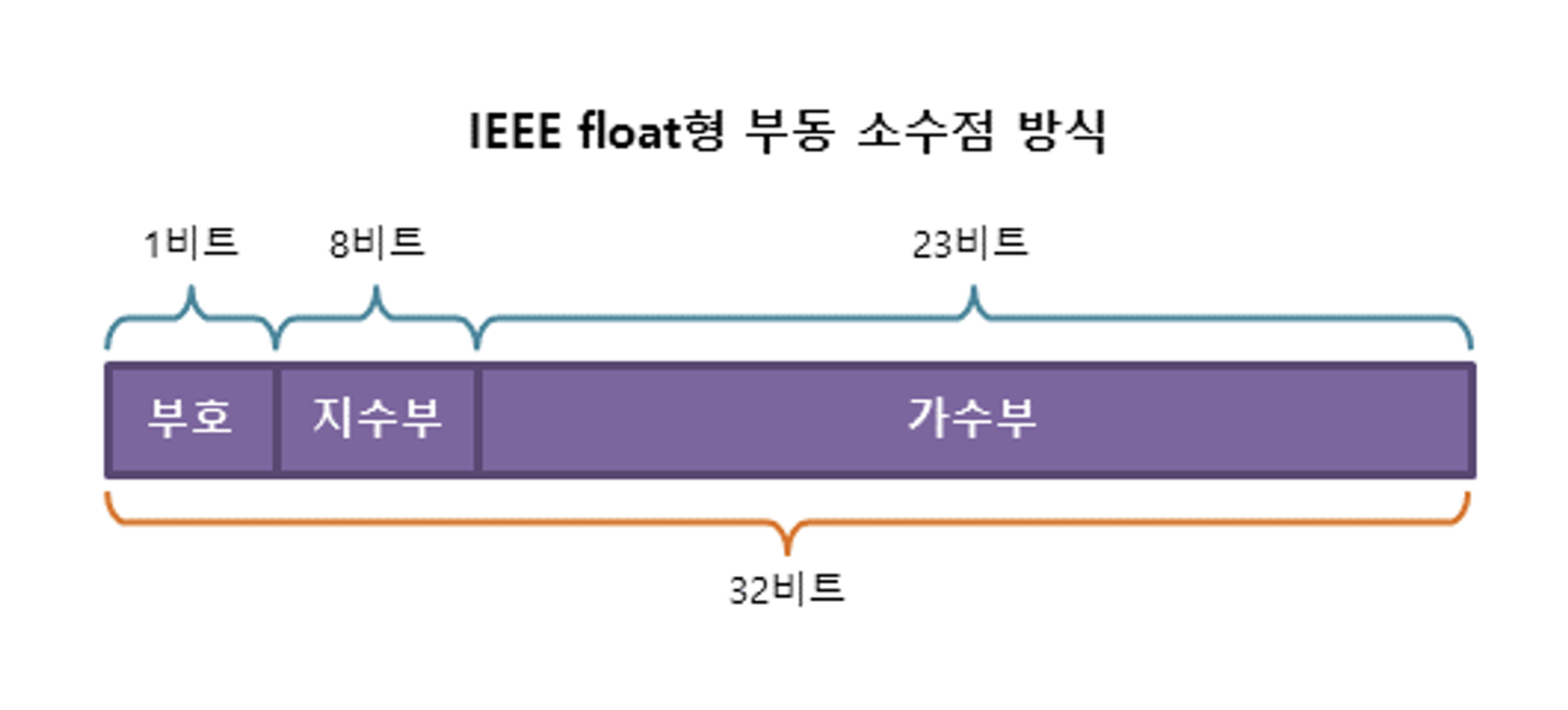
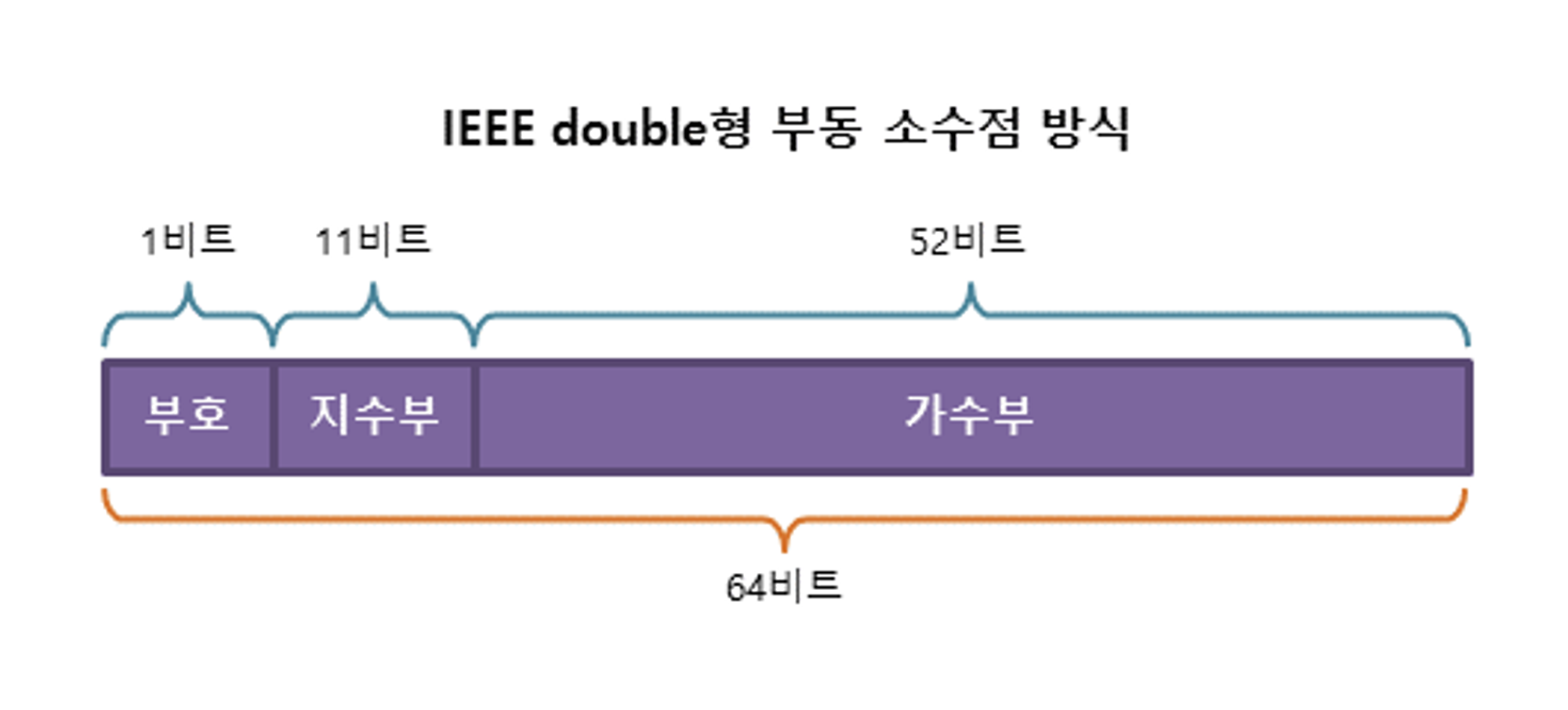
C 언어를 배우다 보면 실수를 표현할 수 있는 데이터 타입에 대해서 배우게 된다. float과 double이 실수를 표현할 수 있는 데이터 타입이며, 부동 소수점 방식을 이용한다. 이 때 꼭 마주하게 되는 그림이 있는데 바로 아래 사진과 같은 float과 double의 지수부, 가수부 표현 그림이다.
지수부와 가수부를 배울 때, 그저 지수부는 지수를 표현하기 위한 부분이고 가수부는 가수를 표현하기 위한 부분이라고만 배웠다. 또한 double이 float에 비해서 정확도가 높은 이유는 가수부에 대해서 표현할 수 있는 범위가 float보다 크기 때문이라고만 배웠다. 그 이후에는 따로 지수부와 가수부에 대해서 고민을 해본 적도 없었고, 시험 공부를 하더라도 이게 나오나 싶은 생각에 외우지도 않고 그냥 넘겼던 기억이 난다.
우리는 학교에서 수에 대해서 이런 표기를 배운 적이 있을 것이다. 예를 들어 라고 하면, 으로 표기할 수 있다. 이런 방법을 과학적 기수법이라고 부른다. 수를 과학적 기수법으로 표현하는 것은 컴퓨터에서 실수를 표현하는 것에 있어서 매우 중요하다.
예를 들어 어떤 수 로 표현 했을 때, 를 가수, 를 밑, 를 지수라고 한다. 이 를 위에서 제시한 사진에 그대로 표현할 수 있다. 는 부호 비트, 는 가수부에, 는 지수부에 기록하게 된다.
의 경우 컴퓨터에서는 0, 1만 이해할 수 있는 2진법을 이용하기 때문에 2로 고정되므로 메모리에 별도로 표기할 필요가 없다.
2. 실수를 메모리에 표현하는 방법
실수를 메모리에 저장하는 것은 크게 어렵지 않다. 위에서 언급한 것과 같이 부호와 가수부, 지수부를 각각 필드에 맞게 할당하면 되기 때문이다. 즉, 과학적 기수법만 잘 나타내면 큰 문제는 없다. 하지만 과학적 기수법으로 수를 나타내기 위해서는 가장 먼저 정규화(Normalization) 과정을 거쳐야 한다.
예를 들어서, 10진수 라고 하는 수에서 부호를 떼고 를 2진수로 나타내면 라는 수가 나타나게 된다. 이 수를 로 만들어 준 후에 과학적 기수법으로 로 나타내어 가수부를 , 지수부를 을 2진수로 표현한 으로 나타내게 되는 것이다.
만일 가수부가 표현 범위를 넘어가면 반올림을 하게 된다. 예를 들면, 23자리까지 표현이 가능하다면 24자리에서 반올림을 하게 된다.
하지만 실제 컴퓨터는 이렇게 과학적 기수법으로 표현한 값을 바로 메모리에 할당하지 않는다. 실제 컴퓨터에서는 지수에 를 더하여 저장하게 된다. 이 때 더하는 값을 편향 값(Bias)라고 부른다. 부호가 있는 데이터 타입의 MSB는 이므로 라고 하는 것은 MSB를 제외한 나머지 비트들이 1이 되는 수를 의미한다. 따라서 8비트를 이용하는 float의 경우 이 편향 값이 되는 것이고, 11비트를 사용하는 double의 경우 이 편향 값이 되는 것이다.
이렇게 편향 값을 더하는 이유는 지수부에 음수 표현을 하지 않도록 하기 위해서이다. 지수부에 음수가 나올 수 있는가? 10진수 의 경우, 2진수로 나타내면 이고 이를 정규화 하게 되면 왼쪽으로 쉬프팅이 일어나기 때문에 지수부는 이 된다.
그렇다면 을 그대로 2의 보수로 나타내어 로 표현하여 (4비트를 기준으로 을 이라 하였다.) 이를 메모리에 넣으면 되지 않는가? 컴퓨터의 입장에서는 크기 비교에 있어서 양수끼리의 비교가 훨씬 수월하기 때문에 음수 값을 없애는 것이 더 낫고, 따라서 음수 값이 들어가는 것을 방지하기 위해 지수부에 편향 값을 더하여 나타내는 것이다.
이렇게 편향 값을 더하게 되면 float의 경우 1~254까지의 지수 표현이 가능하고, double의 경우 1~2046까지 지수 표현이 가능하다. 정리하자면 실수를 메모리에 표현하기 위해서는 정규화 → 과학적 기수법 표기 → 지수부에 편향 값 덧셈의 과정을 거쳐야 한다.
3. 표현 가능 범위 밖의 수들
위 소제목의 마지막 문장을 보면 float은 1~254, double은 1~2046까지의 지수 표현이 가능하다고 했다. 지수부에서의 float 8비트, double 11비트를 감안하면, float은 256개 그리고 double은 2048개의 지수 표현이 가능해야 한다. 그런데 각각의 데이터 타입에서 0과 가장 마지막 수는 왜 지수 표현 가능한 범위에서 빠지게 되었을까?
부동 소수점을 표현하는 방법은 국제전기전자기술자협회라고 하는 IEEE에서 정했으며, 이 때 표현 가능 범위를 넘어서는 값을 표현하기 위해서 0과 가장 마지막 값, 총 2개의 값을 빼서 표현을 하게 되었다.
1) Denormalized Number
지수부 →
가수부 → 이 아닌 수
해당 경우는 표현할 수 있는 가장 작은 지수보다도 더 작은 경우를 의미한다. float을 예를 들어, 지수부에 편향 값을 취하기 전에 float에서 표현할 수 있는 가장 작은 지수 값은 이다. 이 때 Denormalized Number라고 함은 보다 더 작은 수를 의미한다.
2) Infinity
지수부 →
가수부 →
실수를 표현할 때, 부호 비트를 사용할 수 있는 덕분에 음의 무한과 양의 무한을 표현 할 수 있게 되었다.
3) NaN
지수부 →
가수부 → 이 아닌수
, , , , 처럼 값을 엄밀하게 정할 수 없는 것들을 의미한다.