Subjects
<math.h>에는 수학적 연산과 관련된 많은 함수들이 존재한다. 자세히 살펴보면 비슷한 이름들의 함수가 여럿 묶여 있는 것을 볼 수 있는데, 이는 C 언어에 C++에서의 오버로딩 기능이 존재하지 않기 때문이다. C 언어에서 함수를 정의할 때는 받는 인자가 다르더라도 동일한 함수 이름을 사용할 수 없다. 따라서 동일한 기능을 수행하는 함수들임에도 받는 인자에 따라서 함수의 이름을 조금씩 다르게 둔 것이다. 따라서 <math.h>를 뜯어보면 아래에 주어진 함수들이 함수 이름 끝에 f가 붙은 것, 함수 이름 끝에 l이 붙은 것, 아무 것도 붙지 않은 것들로 각 3개씩 존재하는 것을 볼 수 있다.
•
함수 이름 끝에 f가 붙은 것 : 함수의 인자로 float 타입을 받는다.
원 함수 이름에 별도의 명시가 없다면 반환 타입도 float이다.
•
함수 이름 끝에 l이 붙은 것 : 함수의 인자로 long double 타입을 받는다.
원 함수 이름에 별도의 명시가 없다면 반환 타입도 float이다.
•
함수 이름 끝에 아무 것도 붙지 않은 것 : 함수의 인자로 double 타입을 받는다.
원 함수 이름에 별도의 명시가 없다면 반환 타입도 float이다.
라이브러리를 사용하면서 발생한 Error는 math_errhandling이라는 매크로를 이용하여 처리한다. math_errhandling이라는 매크로는 Bitmask 값으로 MATH_ERRNO와 MATH_ERREXCEPT를 사용한다. MATH_ERRNO는 1, MATH_ERREXCEPT는 2의 값을 가진다. 따라서 MATH_ERRNO | MATH_ERREXCEPT는 3이라는 값이 된다. math_errhandling을 이용한 예제는 아래와 같다.
#include <stdio.h> // printf
#include <math.h> // math_errhandling
#include <fenv.h> // feclearexcept, fetestexcept, FE_ALL_EXCEPT, FE_INVALID
int main(void)
{
if (math_errhandling & MATH_ERREXCEPT)
feclearexcept(FE_ALL_EXCEPT);
printf("Error Handling : %d\n", math_errhandling);
printf("Domain Error Value : %f\n", sqrt(-10.0));
if (math_errhandling & MATH_ERREXCEPT)
if (fetestexcept(FE_INVALID))
printf("FE_INVALID raised\n");
return (0);
}
C
복사
MATH_ERRNO에 대해서는 Domain Error가 발생하면 <errno.h>의 errno 값을 EDOM으로 설정하고, Range Error가 발생하면 <errno.h>의 errno 값을 ERANGE로 설정한다. (애초에 범위에 해당하지 않는 값을 이용하는 경우가 Domain Error, 범위에 해당하는 값을 이용했는데 Pole Error, Overflow, Underflow등이 발생한 경우가 Range Error라고 보면 된다.)
MATH_ERREXCEPT에 대해서는 Domain Error가 발생하면 FE_INVALID가 발생하고, Pole Error가 발생하면 FE_DIVBYZERO가 발생하고, Overflow가 발생하면 FE_OVERFLOW가 발생하고, Underflow가 발생하면 FE_UNDERFLOW 가 발생한다.
<math.h>에 존재하는 각 함수의 Domain과 Range는 아래 링크를 참고하자.
1. Trigonometric Functions
1) cos
함수 원형
float cosf(float x);
double cos(double x);
long double cosl(long double x);
C
복사
함수 인자
함수의 인자로 Angle이 아닌 Radian 값을 받는다. 따라서 만일 Angle 값을 갖고 있다면 를 곱하여 Radian으로 변환 후 인자로 넣어줘야 한다. 는 일반적으로 #define을 이용하여 3.14159265값으로 두고 쓰면 된다.
반환 값
x라는 Radian에 대한 값을 반환
2) sin
함수 원형
float sinf(float x);
double sin(double x);
long double sinl(long double x);
C
복사
함수 인자
함수의 인자로 Angle이 아닌 Radian 값을 받는다. 따라서 만일 Angle 값을 갖고 있다면 를 곱하여 Radian으로 변환 후 인자로 넣어줘야 한다. 는 일반적으로 #define을 이용하여 3.14159265값으로 두고 쓰면 된다.
반환 값
x라는 Radian에 대한 값을 반환
3) tan
함수 원형
float tanf(float x);
double tan(double x);
long double tan(long double x);
C
복사
함수 인자
함수의 인자로 Angle이 아닌 Radian 값을 받는다. 따라서 만일 Angle 값을 갖고 있다면 를 곱하여 Radian으로 변환 후 인자로 넣어줘야 한다. 는 일반적으로 #define을 이용하여 3.14159265값으로 두고 쓰면 된다.
반환 값
x라는 Radian에 대한 값을 반환
4) acos
함수 원형
float acosf(float x);
double acos(double x);
long double acosl(long double x);
C
복사
함수 인자
을 구간으로 하는 Radian 값 (구간 외 값이 들어가면 Domain이 맞지 않는 것이므로 Domain Error가 발생한다.)
반환 값
x라는 Radian에 대해 을 수행하여 을 구간으로 하는 Radian 값을 반환 (Angle로 이용하려면 을 곱하여 이용한다.)
5) asin
함수 원형
float asinf(float x);
double asin(double x);
long double asinl(long double x);
C
복사
함수 인자
을 구간으로 하는 Radian 값 (구간 외 값이 들어가면 Domain이 맞지 않는 것이므로 Domain Error가 발생한다.)
반환 값
x라는 Radian에 대해 을 수행하여 을 구간으로 하는 Radian 값을 반환 (Angle로 이용하려면 을 곱하여 이용한다.)
6) atan
함수 원형
float atanf(float x);
double atan(double x);
long double atanl(long double x);
C
복사
함수 인자
다른 arc함수들처럼 Domain이 있는 것은 아니다. 어떤 실수 값도 인자로 사용될 수 있다. 인자로 들어간 값은 Radian 값이다.
반환 값
x라는 Radian에 대해 을 수행하여 을 구간으로 하는 Radian 값을 반환 (Angle로 이용하려면 을 곱하여 이용한다.)
참고
부호의 모호성 때문에 atan이라는 함수는 값에 의해 떨어지는 각이 어느 사분면인지 명확히 할 수 없다. 따라서 부분적으로 인자를 받는 atan2 함수를 대안으로 이용한다.
7) atan2
함수 원형
float atan2f(float y, float x);
double atan2(double y, double x);
long double atan2l(long double y, long double x);
C
복사
함수 인자
y는 나타내려는 좌표의 축 위의 값을 의미하고, x는 나타내려는 좌표의 축 위의 값을 의미한다. (두 값이 모두 0으로 주어지면 Domain Error가 발생한다.) 로 계산되어 Radian 값으로 이용된다.
반환 값
라는 Radian에 대해 을 수행하여 을 구간으로 하는 Radian 값을 반환 (Angle로 이용하려면 을 곱하여 이용한다.)
2. Hyperbolic Functions
1) cosh
함수 원형
float coshf(float x);
double cosh(double x);
long double coshl(long double x);
C
복사
함수 인자
쌍곡각을 나타내는 값을 인자로 한다.
반환 값
쌍곡각에 대해 쌍곡 코사인을 적용한 값을 반환 (반환 값이 너무 커서 반환 타입으로 표현이 불가능한 경우에는 부호 값이 붙은 HUGE_VAL 혹은 HUGE_VALF 혹은 HUGE_VALL을 반환하고 Range Error가 발생한다.)
2) sinh
함수 원형
float sinhf(float x);
double sinh(double x);
long double sinhl(long double x);
C
복사
함수 인자
쌍곡각을 나타내는 값을 인자로 한다.
반환 값
쌍곡각에 대해 쌍곡 사인을 적용한 값을 반환 (반환 값이 너무 커서 반환 타입으로 표현이 불가능한 경우에는 부호 값이 붙은 HUGE_VAL 혹은 HUGE_VALF 혹은 HUGE_VALL을 반환하고 Range Error가 발생한다.)
3) tanh
함수 원형
float tanhf(float x);
double tanh(double x);
long double tanhl(long double x);
C
복사
함수 인자
쌍곡각을 나타내는 값을 인자로 한다.
반환 값
쌍곡각에 대해 쌍곡 탄젠트를 적용한 값을 반환
4) acosh
함수 원형
float acoshf(float x);
double acosh(double x);
long double acoshl(long double x);
C
복사
함수 인자
1보다 작은 값만 아니면 된다. 1보다 작은 값이 들어가면 Domain Error가 발생한다.
반환 값
를 구간으로 하는 음수가 아닌 쌍곡 코사인의 영역 값을 Radian으로 반환
5) asinh
함수 원형
float asinhf(float x);
double asinh(double x);
long double asinhl(long double x);
C
복사
함수 인자
어떤 실수 값이든 인자로 사용할 수 있다.
반환 값
쌍곡 사인의 영역 값을 Radian으로 반환
6) atanh
함수 원형
float atanhf(float x);
double atanh(double x);
long double atanhl(long double x);
C
복사
함수 인자
을 구간으로 하는 값을 인자로 받는다. 이외의 값이 들어가면 Domain Error가 발생한다. 또한 -1 혹은 +1이 인자로 들어가는 경우엔 Pole Error가 발생할 수 있다.
반환 값
쌍곡 탄젠트의 영역 값을 Radian으로 반환
3. Exponential and Logarithmic Functions
1) exp
함수 원형
float expf(float x);
double exp(double x);
long double expl(long double x);
C
복사
함수 인자
어떤 실수 값이든 인자로 사용할 수 있다.
반환 값
인자로 받은 x를 이용하여 값을 계산하여 반환 (반환 값이 너무 커서 반환 타입으로 표현이 불가능한 경우에는 부호 값이 붙은 HUGE_VAL 혹은 HUGE_VALF 혹은 HUGE_VALL을 반환하고 Range Error가 발생한다.)
2) frexp
함수 원형
float frexpf(float x, int *exp);
double frexp(double x, int *exp);
long double frexpl(long double x, int *exp);
C
복사
함수 인자
x는 함수 수행을 통해 분해될 값을 의미하고, exp는 함수 수행을 통해 저장될 의 지수 값이다. 반환 값이 있는데도 별도로 exp를 포인터로 넘기는 것을 보아 주로 다루고 싶은 값이 2개임을 알 수 있다.
반환 값
절대값이 를 구간으로 하는 부동 소수점을 반환 (2의 지수로 exp를 사용하여 반환 값을 곱하면 x가 된다.)
참고
반환 값으로 사용되는 부동 소수점을 Significand라고 부른다. frexp 함수는 인자로 받은 값 x을 Significand와 exp로 나누어 표현하고자 한다. 즉, 이다. 만일 x로 0이 들어오면 Significand와 exp는 모두 0이 된다. 만일 x가 음수로 들어오면, Significand도 음수로 반환된다.
3) ldexp
함수 원형
float ldexpf(float x, int exp);
double ldexp(double x, int exp);
long double ldexpl(long double x, int exp);
C
복사
함수 인자
x는 함수 수행에 사용되는 Significand이고, exp는 함수 수행에 사용될 2의 지수 값이다.
반환 값
인자로 받은 x와 exp를 이용하여 를 계산한 결과를 반환 (반환 값이 너무 커서 반환 타입으로 표현이 불가능한 경우에는 부호 값이 붙은 HUGE_VAL 혹은 HUGE_VALF 혹은 HUGE_VALL을 반환하고 Range Error가 발생한다.)
참고
frexp 함수가 분해하는 함수였다면, ldexp는 합성하는 함수라고 보면 된다.
4) log
함수 원형
float logf(float x);
double log(double x);
long double log(long double x);
C
복사
함수 인자
인자 값이 음수라면 Domain Error가 발생한다. 인자가 0일 때는 Implementation-Defined Behavior여서 Pole Error가 나타날 수도 있다.
반환 값
인자로 받은 x를 밑을 로하는 자연 로그를 취하여 반환
5) log10
함수 원형
float log10f(float x);
double log10(double x);
long double log10l(long double x);
C
복사
함수 인자
인자 값이 음수라면 Domain Error가 발생한다. 인자가 0일 때는 Implementation-Defined Behavior여서 Pole Error가 나타날 수도 있다.
반환 값
인자로 받은 x를 밑을 으로 하는 로그를 취하여 반환
6) modf
함수 원형
float modff(float x, float *intpart);
double modf(double x, double *intpart);
long double modfl(long double x, long double *intpart);
C
복사
함수 인자
정수부와 소수부로 나누고자 하는 값 x와 나눈 정수부를 저장할 intpart라는 포인터를 인자로 받는다. intpart의 타입은 x의 타입과 동일하게 받으며, 부호 역시 x와 동일하게 저장된다. (나누고자 하는 값 x가 음수면 intpart가 음수로 저장된다.)
반환 값
인자 x의 소수부를 반환 (소수부의 부호 역시 x와 동일하다.)
참고
정수부와 소수부의 부호 모두 x의 부호와 동일하다. 정수부를 저장하는 intpart가 int 타입을 쓰지 않고 실수 표현을 위한 타입을 사용하는 것은 소수부와의 연산 편의성과 그 의도 때문이다.
7) exp2
함수 원형
float exp2f(float x);
double exp2(double x);
long double exp2l(long double x);
C
복사
함수 인자
지수승으로 사용될 x를 인자로 받는다.
반환 값
인자 x를 이용하여 의 지수승을 반환 (반환 값이 너무 커서 반환 타입으로 표현이 불가능한 경우에는 부호 값이 붙은 HUGE_VAL 혹은 HUGE_VALF 혹은 HUGE_VALL을 반환하고 Range Error가 발생한다.)
8) expm1
함수 원형
float expm1f(float x);
double expm1(double x);
long double expm1l(long double x);
C
복사
함수 인자
지수승으로 사용될 x를 인자로 받는다.
반환 값
인자 x를 이용하여 의 지수승을 만들고 1을 뺀 값을 반환 (반환 값이 너무 커서 반환 타입으로 표현이 불가능한 경우에는 부호 값이 붙은 HUGE_VAL 혹은 HUGE_VALF 혹은 HUGE_VALL을 반환하고 Range Error가 발생한다.)
참고
expm1 함수의 이름에서 m1은 Minus One을 의미한다. 인자로 받은 x의 값이 그리 크지 않은 값이라면, exp 함수를 이용한 exp(x) - 1보다 더 정확할 수 있어서 이를 이용하는게 좋다.
9) ilogb
함수 원형
int ilogbf(float x);
int ilogb(double x);
int ilogbl(long double x);
C
복사
함수 인자
함수의 의도대로라면 인자에 절대값을 이용하여 로그를 취하기 때문에 어떤 값이 들어와도 무방하다.
반환 값
인자로 받은 x의 절대값에 밑을 FLT_RADIX로하는 로그를 취해 정수부를 반환 (반환 값이 너무 커서 반환 타입으로 표현이 불가능한 경우에는 부호 값이 붙은 HUGE_VAL 혹은 HUGE_VALF 혹은 HUGE_VALL을 반환하고 Range Error가 발생한다. 또한 인자로 받은 값이 0, infinity, NaN이라면 Domain Error 혹은 Range Error가 발생할 수 있다.)
참고
인자로 받은 x값이 0이면 FP_ILOGB0이 반환된다. (FP_ILOGB0은 매크로 상수로 정의되어 있다.)
인자로 받은 값이 infinity이면 INT_MAX가 반환된다.
인자로 받은 x값이 NaN이면 FP_ILOGBNAN이 반환된다. (FP_ILOGBNAN은 매크로 상수로 정의되어 있다.)
인자로 받은 x값이 Normal이라면 FLT_RADIX를 밑으로하는 로그를 취하여 정수부를 반환한다.
인자로 받은 x값이 Subnormal이면 Normalize된 표현 (음의 지수)의 값이 반환된다.
isnormal이라는 매크로 함수가 있는데 이는 0, infinity, NaN, subnormal에 대해서 0을 반환하고 그 외의 값에 대해선 1을 반환하는 함수이다. 여기서의 Normal과 Subnormal은 isnormal의 판별을 따른다.
FLT_RADIX는 일반적으로 2로 정의되어 있다.
내부적으로 인자로 들어온 값 x를 표현하기 위해 와 를 이용한다. 는 1.0에서 FLT_RADIX 사이의 값을 갖고 있는데, 절대값을 취한 양수 x를 표현할 때 와 같이 나타난다.
10) log1p
함수 원형
float log1pf(float x);
double log1p(double x);
long double log1pl(long double x);
C
복사
함수 인자
-1보다 작은 값이 들어가면 Domain Error가 발생한다. 인자가 -1일 때는 Implementation-Defined Behavior여서 Pole Error가 나타날 수도 있다.
반환 값
인자로 받은 x 값에 1을 더하여 밑을 로 하는 로그를 취한 값을 반환
참고
log1p 함수의 이름에서 1p는 Plus One을 의미한다. 인자로 받은 x의 값이 그리 크지 않은 값이라면, log 함수를 이용한 log(1+p)보다 더 정확할 수 있어서 이를 이용하는게 좋다.
11) log2
함수 원형
float log2f(float x);
double log2(double x);
long double log2l(long double x);
C
복사
함수 인자
인자가 음수라면 Domain Error가 발생한다. 인자가 0일 때는 Implementation-Defined Behavior여서 Pole Error가 나타날 수도 있다.
반환 값
인자로 받은 x값을 이용하여 밑을 로하는 로그를 취한 값을 반환
12) logb
함수 원형
float logbf(float x);
double logb(double x);
long double logbl(long double x);
C
복사
함수 인자
인자가 0일 때는 Domain Error 혹은 Pole Error가 발생하거나Implementation에 따라 Error가 발생하지 않을 수도 있다.
반환 값
인자로 받은 x값에 절대값을 취하여 밑을 FLT_RADIX로하는 로그를 취한 값을 반환
참고
인자로 들어온 x값이 양수라면 그 동작이 log 함수와 동일하다. (FLT_RADIX는 일반적으로 대부분의 플랫폼에서 2라는 값을 갖기 때문이다.)
13) scalbn
함수 원형
float scalbnf(float x, int n);
double scalbn(double x, int n);
long double scalbnl(long double x, int n);
C
복사
함수 인자
x는 Significand를 의미하는 실수이고, n은 제곱 연산을 수행할 exp에 해당한다.
반환 값
FLT_RADIX를 인자로 받은 n만큼 제곱하여 인자로 받은 x를 곱한 값을 반환 (반환 값이 너무 커서 반환 타입으로 표현이 불가능한 경우에는 부호 값이 붙은 HUGE_VAL 혹은 HUGE_VALF 혹은 HUGE_VALL을 반환하고 Range Error가 발생한다.)
참고
인데 일반적으로 대부분의 플랫폼에서 FLT_RADIX는 2라는 값을 갖기 떄문에 scalbn이라는 함수는 ldexp 함수와 그 기능이 동일하다.
14) scalbln
함수 원형
float scalblnf(float x, long int n);
double scalbln(double x, long int n);
long double scalblnl(long double x, long int n);
C
복사
함수 인자
x는 Significand를 의미하는 실수이고, n은 제곱 연산을 수행할 exp에 해당한다.
반환 값
FLT_RADIX를 인자로 받은 n만큼 제곱하여 인자로 받은 x를 곱한 값을 반환 (반환 값이 너무 커서 반환 타입으로 표현이 불가능한 경우에는 부호 값이 붙은 HUGE_VAL 혹은 HUGE_VALF 혹은 HUGE_VALL을 반환하고 Range Error가 발생한다.)
참고
이다. scalbln 함수는 scalbn 함수와 달리 exp에 대한 인자 n을 long int로 받는다.
4. Power Functions
1) pow
함수 원형
float powf(float base, float exponent);
double pow(double base, double exponent);
long double powl(long double base, long double exponent);
C
복사
함수 인자
인자는 이름 그대로 base가 지수의 밑으로, exponent가 지수의 승을 의미한다.
반환 값
를 반환
참고
base가 Finite인데 음수이고 exponent가 Finite인데 정수가 아니라면, Domain Error가 발생한다.
base와 exponent가 모두 0이라면 Implementation에 따라 몇 경우에는 Domain Error가 발생할 수 있다.
base가 0이고 exponent가 음수면, Domain Error 혹은 Pole Error가 발생하거나Implementation에 따라 Error가 발생하지 않을 수도 있다.
함수 수행의 결과가 너무 크거나 작으면 Range Error가 발생할 수도 있다.
isfinite이라는 매크로 함수가 있는데, 이는 주어진 수가 finite이면 1을 반환하고 finite하지 않다면 0을 반환하는 함수이다. 여기서의 Finite은 isfinite의 판별을 따른다.
2) sqrt
함수 원형
float sqrtf(float x);
double sqrt(double x);
long double sqrtl(long double x);
C
복사
함수 인자
인자가 음수라면 Domain Error가 발생한다.
반환 값
인자로 받은 x의 제곱근을 반환
3) cbrt
함수 원형
float cbrtf(float x);
double cbrt(double x);
long double cbrtl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x에 대한 세제곱근을 반환
4) hypot
함수 원형
float hypotf(float x, float y);
double hypot(double x, double y);
long double hypotl(long double x, long double y);
C
복사
함수 인자
직각 삼각형을 이루고 있는 변들 중 빗변을 제외한 나머지 두 변 x, y를 인자로 받는다.
반환 값
인자로 받은 x, y값에 대해 를 계산하여 빗변의 길이를 반환 (반환 값이 너무 커서 반환 타입으로 표현이 불가능한 경우에는 부호 값이 붙은 HUGE_VAL 혹은 HUGE_VALF 혹은 HUGE_VALL을 반환하고 Range Error가 발생한다.)
5. Error and Gamma Functions
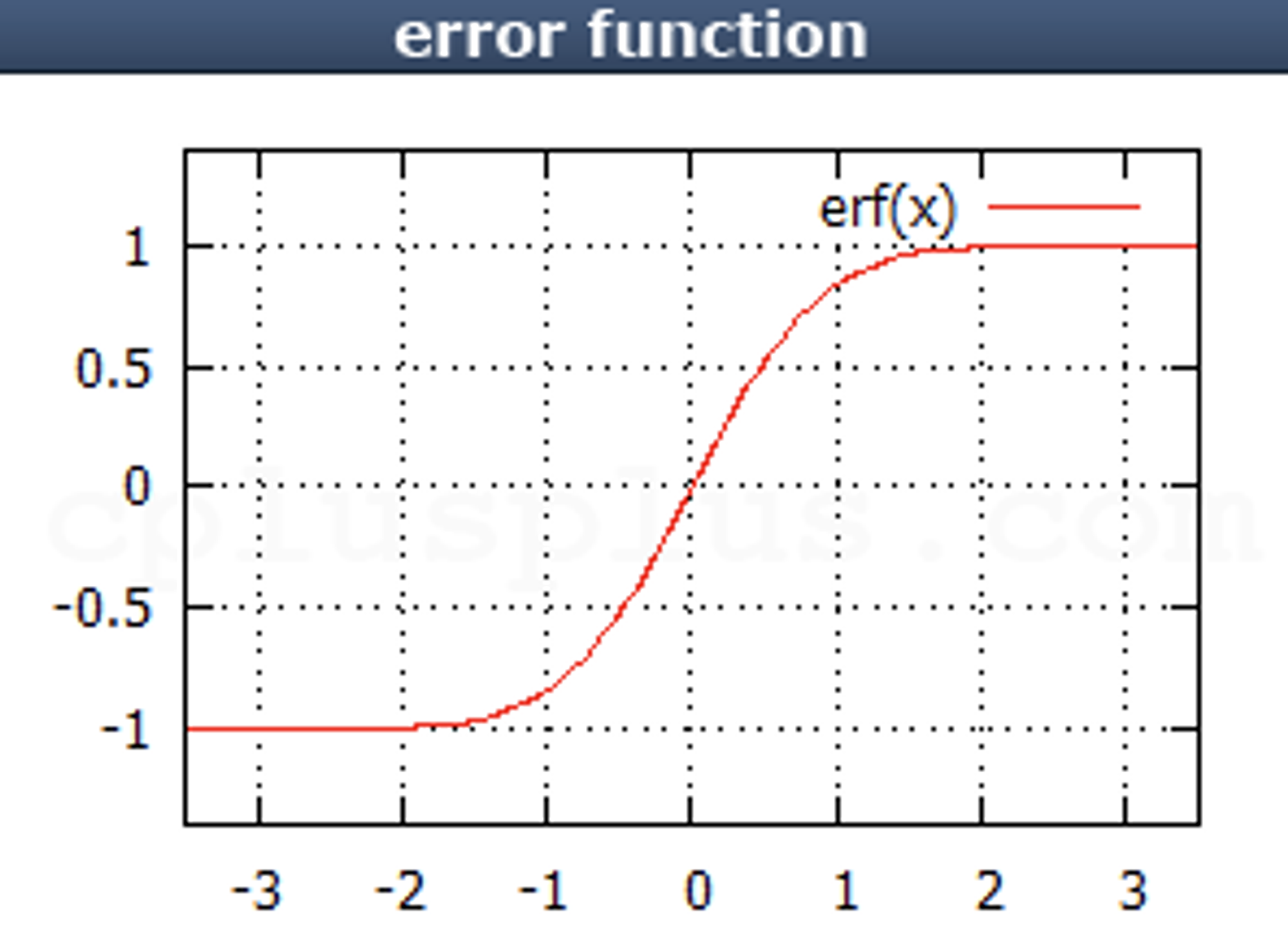
1) erf
함수 원형
float erff(float x);
double erf(double x);
long double erfl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
Error Function을 처리한 값을 반환
참고
Error Function의 수식은 다음과 같다.
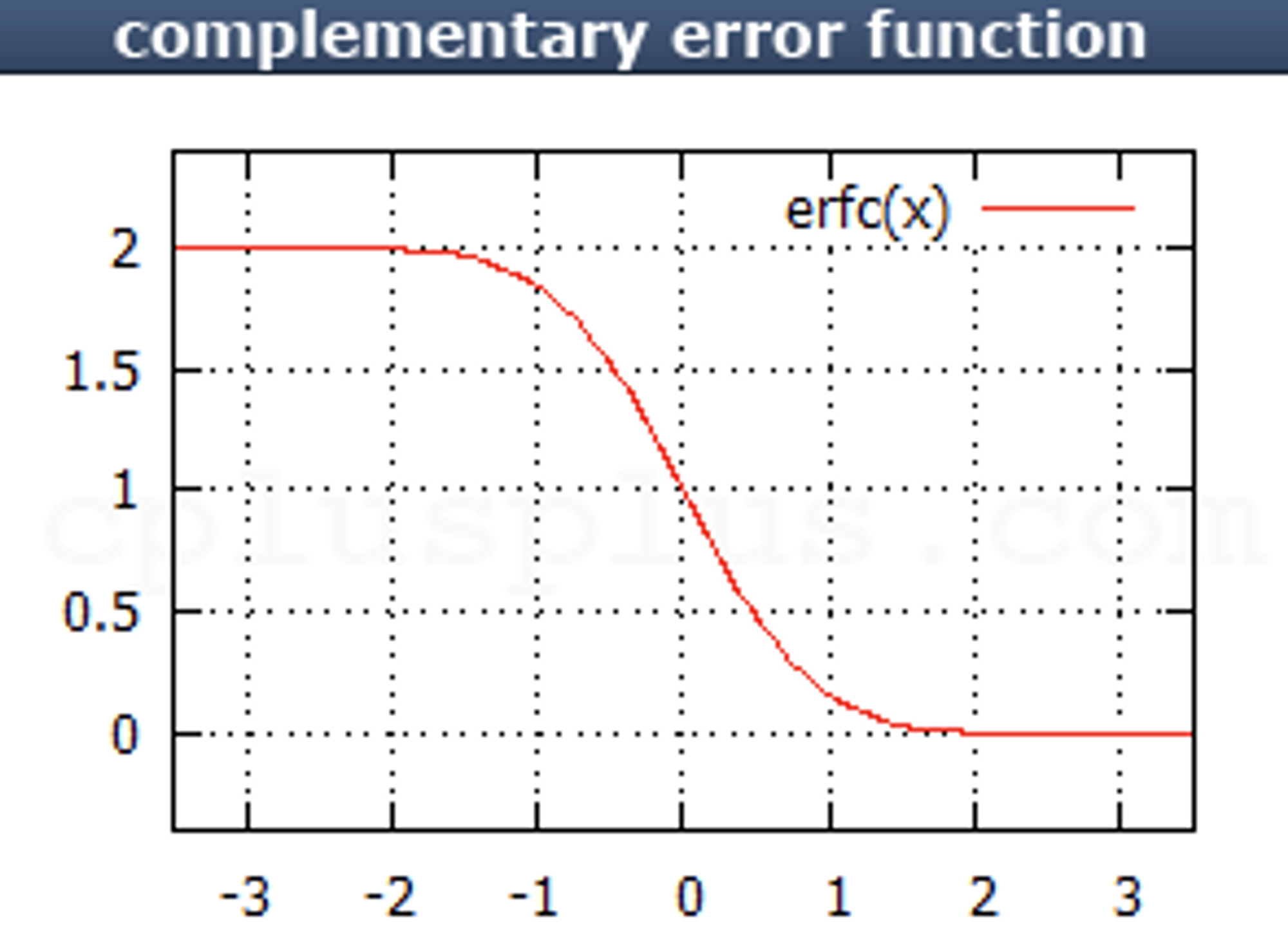
2) erfc
함수 원형
float erfcf(float x);
double erfc(double x);
long double erfcl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있지만 너무 큰 값을 인자로 받게 되면 Underflow로 인한 Range Error가 발생한다.
반환 값
Complementary Error Function을 처리한 값을 반환
참고
Complementary Error Function의 수식은 다음과 같다.
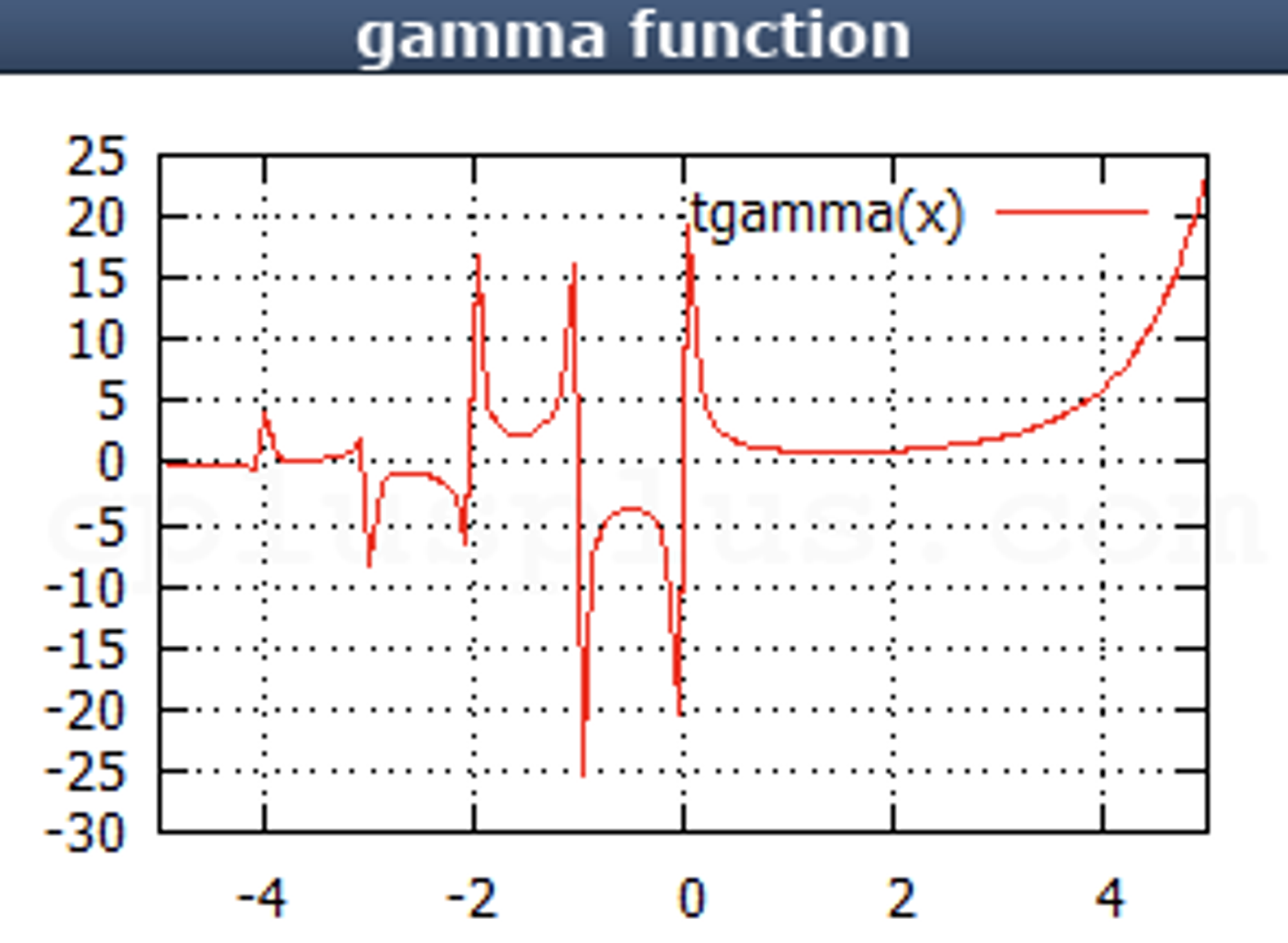
3) tgamma
함수 원형
float tgammaf(float x);
double tgamma(double x);
long double tgammal(long double x);
C
복사
함수 인자
인자로 받은 값이 0 혹은 음의 정수라면 함수가 점근성을 띄기 때문에 Domain Error 혹은 Pole Error가 발생하거나Implementation에 따라 Error가 발생하지 않을 수도 있다. 또한 인자로 받은 값이 너무 크다면 Overflow로 인한 Range Error가 발생할 수 있고, 인자로 받은 값이 너무 작다면 Underflow로 인한 Range Error가 발생할 수 있다.
반환 값
Gamma Function을 처리한 값을 반환
참고
Gamma Function의 수식은 다음과 같이 표기한다.
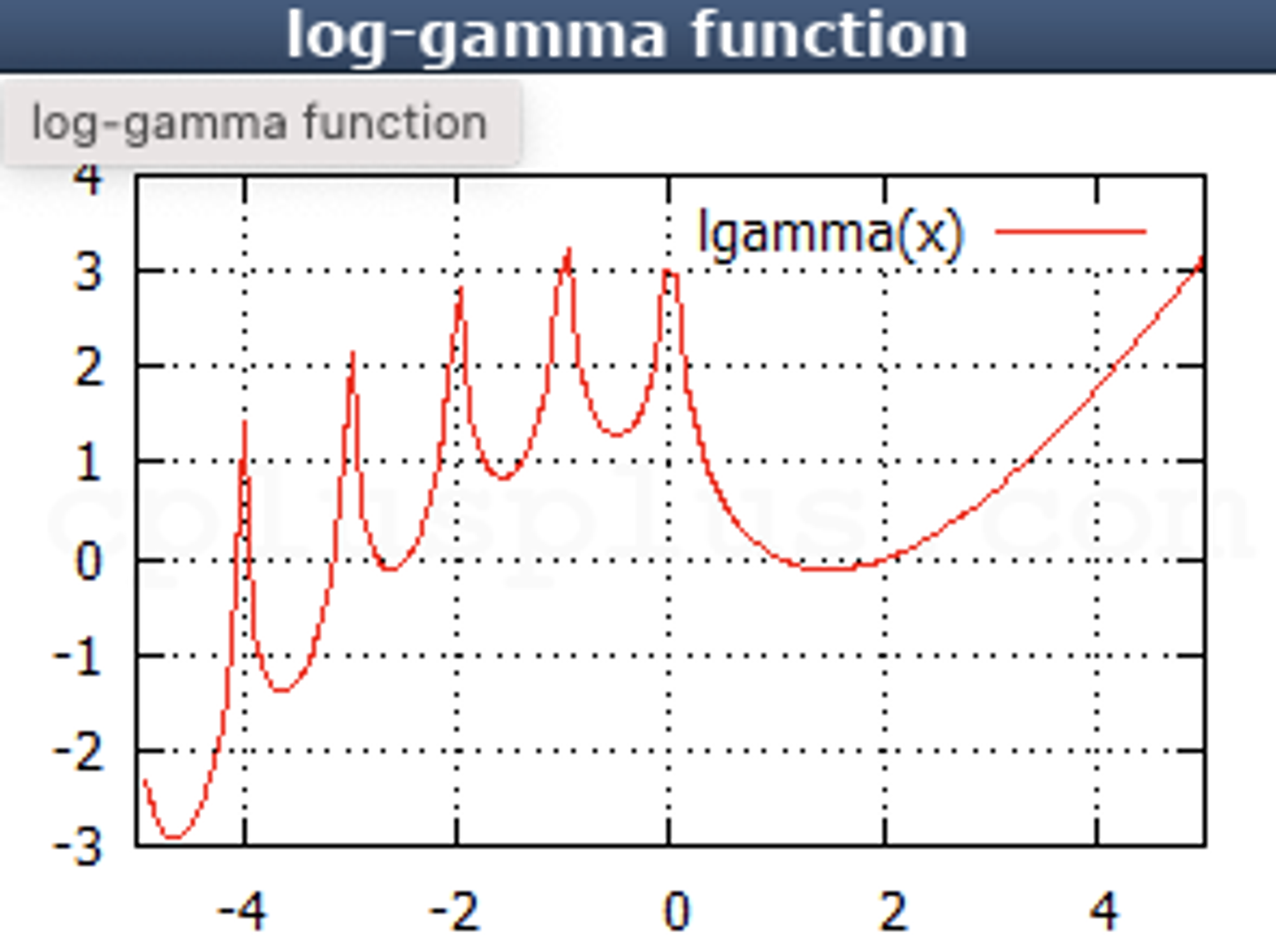
4) lgamma
함수 원형
float lgammaf(float x);
double lgamma(double x);
long double lgammal(long double x);
C
복사
함수 인자
인자로 받은 값이 0 혹은 음의 정수라면 함수가 점근성을 띄기 때문에 Domain Error 혹은 Pole Error가 발생하거나Implementation에 따라 Error가 발생하지 않을 수도 있다. 또한 인자로 받은 값이 너무 크다면 Overflow로 인한 Range Error가 발생할 수 있다.
반환 값
Log Gamma Function을 처리한 값을 반환
참고
Log Gamma Function의 수식은 다음과 같이 표기한다.
6. Rounding and Remainder Functions
1) ceil
함수 원형
float ceilf(float x);
double ceil(double x);
long double ceill(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x보다 작지 않은 정수 값을 부동 소수점으로 반환
참고
올림을 수행한다.
2) floor
함수 원형
float floorf(float x);
double floor(double x);
long double floorl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x보다 크지 않은 정수 값을 부동 소수점으로 반환
참고
내림을 수행한다.
3) fmod
함수 원형
float fmodf(float numer, float denom);
double fmod(double numer, double denom);
long double fmodl(long double numer, long double denom);
C
복사
함수 인자
두 수의 나눗셈에서 분모 (Numerator)를 의미하는 numer, 분자 (Denominator)를 의미하는 denom을 인자로 받는다. (denom의 값이 0이면, Implementation에 따라 0을 반환하거나 Domain Error가 발생할 수 있다.)
반환 값
의 나머지를 부동 소수점으로 반환
참고
fmod 함수의 연산 결과는 이다. 이 때의 은 의 몫인데, 이 몫은 trunc된 값이다. fmod와 비슷한 함수로는 remainder라는 함수가 있는데, remainder는 몫에 대해서 trunc를 사용하지 않고 round된다. trunc는 버림을 round는 반올림을 의미한다.
4) trunc
함수 원형
float truncf(float x);
double trunc(double x);
long double truncl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x를 크기로 보았을 때, 그 값보다보다 크지 않은 정수 값을 부동 소수점을 반환 (부호는 동일하게 유지한다.)
참고
버림을 수행한다.
5) round
함수 원형
float roundf(float x);
double round(double x);
long double roundl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x에 대해 반올림한 값을 부동 소수점으로 반환
6) lround
함수 원형
long int lroundf(float x);
long int lround(double x);
long int lroundl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x에 대해 반올림한 값을 long int로 casting하여 반환
참고
반올림한 값이 반환 타입의 범위를 넘는 경우, 반환 값은 Unspecified Behavior이고 Domain Error 혹은 Overflow로 인한 Range Error가 발생하거나Implementation에 따라 Error가 발생하지 않을 수도 있다. 반환 타입이 long int이다.
7) llround
함수 원형
long long int llroundf(float x);
long long int llround(double x);
long long int llroundl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x에 대해 반올림한 값을 long long int로 casting하여 반환
참고
반올림한 값이 반환 타입의 범위를 넘는 경우, 반환 값은 Unspecified Behavior이고 Domain Error 혹은 Overflow로 인한 Range Error가 발생하거나Implementation에 따라 Error가 발생하지 않을 수도 있다. 반환 타입이 long long int이다.
8) rint
함수 원형
float rintf(float x);
double rint(double x);
long double rintl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x에 대해 반올림한 값을 부동 소수점으로 반환
참고
Implementation에 따라 반환 값이 인자 x와 다른 경우 FE_INEXACT라는 exception이 발생할 수도 있다.
반올림 방식은 현재 설정된 Rounding Direction Mode를 따른다.
9) lrint
함수 원형
long int lrintf(float x);
long int lrint(double x);
long int lrintl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x에 대해 반올림한 값을 long int로 casting하여 반환
참고
Implementation에 따라 반환 값이 인자 x와 다른 경우 FE_INEXACT라는 exception이 발생할 수도 있다.
반올림 방식은 현재 설정된 Rounding Direction Mode를 따른다.
반올림한 값이 반환 타입의 범위를 넘는 경우, 반환 값은 Unspecified Behavior이고 Domain Error 혹은 Overflow로 인한 Range Error가 발생하거나Implementation에 따라 Error가 발생하지 않을 수도 있다. 반환 타입이 long int이다.
10) llrint
함수 원형
long long int llrintf(float x);
long long int llrint(double x);
long long int llrintl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x에 대해 반올림한 값을 long long int로 casting하여 반환
참고
Implementation에 따라 반환 값이 인자 x와 다른 경우 FE_INEXACT라는 exception이 발생할 수도 있다.
반올림 방식은 현재 설정된 Rounding Direction Mode를 따른다.
반올림한 값이 반환 타입의 범위를 넘는 경우, 반환 값은 Unspecified Behavior이고 Domain Error 혹은 Overflow로 인한 Range Error가 발생하거나Implementation에 따라 Error가 발생하지 않을 수도 있다. 반환 타입이 long int이다.
11) nearbyint
함수 원형
float nearbyintf(float x);
double nearbyint(double x);
long double nearbyintl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x에 대해 반올림한 값을 부동 소수점으로 반환
참고
nearbyint 함수는 rint와 달리, 인자로 받은 값이 반환 값과 다르다고 해서 FE_INEXACT라는 exception을 발생시키진 않는다.
rint와 마찬가지로 반올림 방식은 현재 설정된 Rounding Direction Mode를 따른다.
12) remainder
함수 원형
float remainderf(float numer, float denom);
double remainder(double numer, double denom);
long double remainderl(long double numer, long double denom);
C
복사
함수 인자
두 수의 나눗셈에서 분모 (Numerator)를 의미하는 numer, 분자 (Denominator)를 의미하는 denom을 인자로 받는다. (denom의 값이 0이면, Implementation에 따라 0을 반환하거나 Domain Error가 발생할 수 있다.)
반환 값
의 나머지를 부동 소수점으로 반환
참고
remainder 함수의 연산 결과는 이다. 이 때의 은 의 몫인데, 이 몫은 round된 값이다. remainder와 비슷한 함수로는 fmod라는 함수가 있는데, fmod는 몫에 대해서 round를 사용하지 않고, trunc한다. round는 반올림을 trunc는 버림을 의미한다.
13) remquo
함수 원형
float remquof(float numer, float denom, int *quot);
double remquo(double numer, double denom, int *quot);
long double remquol(long double numer, long double denom, int *quot);
C
복사
함수 인자
두 수의 나눗셈에서 분모 (Numerator)를 의미하는 numer, 분자 (Denominator)를 의미하는 denom을 인자로 받는다. 추가적으로 몫을 저장할 quot라는 인자를 포인터로 받는다. (denom의 값이 0이면, Implementation에 따라 0을 반환하거나 Domain Error가 발생할 수 있다.)
반환 값
의 나머지를 부동 소수점으로 반환
참고
몫과 나머지를 구하는 방식이 remainder 함수의 방식과 동일하다. 즉, trunc가 아닌 round를 사용한다.
round vs rint vs nearbyint 그리고 Rounding Direction Mode
round, rint, nearbyint는 모두 반올림을 수행하는 함수이다. 우선 rint와 nearbyint의 차이는 반환 값과 인자로 사용된 값이 서로 다를 때 FE_INEXACT라는 exception을 내냐 안 내냐의 차이만 있을 뿐, 반올림 수행의 경우에는 현재 설정된 Rounding Direction Mode를 따른다. 하지만 round 함수는 Rounding Direction Mode를 고려하지 않아 고정된 방식으로 우리가 알고 있는 방식의 반올림만을 수행한다.
rint와 nearbyint 함수가 수행할 반올림 방식에는 어떤 것들이 있을까? 이는 <fenv.h>를 찾아보면 매크로로 정의되어 있다. 현재 설정되어 있는 Rounding Direction Mode를 알아내는 방법은 <fenv.h>에 있는 fegetround라는 함수를 이용하는 것이고, Rounding Direction Mode를 설정하는 방법은 <fenv.h>에 있는 fesetround라는 함수를 이용하면 된다. Implementation에 따라 다르긴 하지만 Default Mode는 FE_TONEAREST이다.
FE_TONEAREST - Round to Neareast (0x0000)
FE_DOWNWARD - Round Downward (0x0400)
FE_UPWARD - Round Upward (0x0800)
FE_TOWARDZERO - Round toward Zero (0x0c00)
7. Floating-Point Manipulation Functions
1) copysign
함수 원형
float copysignf(float x, float y);
double copysign(double x, double y);
long double copysignl(long double x, long double y);
C
복사
함수 인자
x는 따온 부호 값을 적용하여 결과로 낼 인자이고, y는 부호 값을 따올 인자이다.
반환 값
y의 부호를 x에 적용하여 반환
2) nan
함수 원형
float nanf(const char *tagp);
double nan(const char *tagp);
long double nanl(const char *tagp);
C
복사
함수 인자
Implementation-Defined인 C-string을 인자로 받는다.
반환 값
double 타입으로 된 Quite NaN 값을 반환
참고
NaN이라고 하는 것은 이나 음수의 제곱근과 같이 Undefined 혹은 표현할 수 없는 값을 부동 소수점으로 나타낸 것이다.
만일 nan 함수에 인자로 주어진 C-string이 ""와 같이 널 문자열 (빈 문자열)일 경우, 일반적인 NaN 값을 반환한다. (이 결과는 strtod 함수에 "NaN"이라는 C-string 인자를 준 것과 같은 결과이다.) 인자로 사용되는 C-string은 라이브러리 구현에 따라 특정 방식으로 구현된 다른 NaN 값을 구별하는데 사용될 수 있다. nan 함수의 경우에는 Quiet NaN을 다룬다. 다른 NaN으로는 Signaling NaN이 있다.
Quiet NaN이라함은 프로그램이 NaN을 직접 만나기 전까지 별도로 이상하다고 지시를 하지 않는 NaN이라고 보면 된다. 부동 소수점을 처리하는 FPU (Floating Point Unit)으로부터 별도의 신호를 받은 것이 아니기 때문에 컴퓨팅 연산이 지속된다. 반면에 Signaling NaN의 경우에는 FPU로부터 exception 형태로 신호를 보내게 된다. 각 qNaN과 sNaN의 활용은 사용에 따라 다르겠지만 간단한 예시는 아래 링크에서 찾아볼 수 있다.
3) nextafter
함수 원형
float nextafterf(float x, float y);
double nextafter(double x, double y);
long double nextafterl(long double x, long double y);
C
복사
함수 인자
기준 값을 의미하는 x, 근사값 산출을 위한 방향이 y를 의미한다.
반환 값
일 때는 실수로 표현할 수 있는 수 중에서 현재 보다 바로 작은 실수, 일 때는 실수로 표현할 수 있는 수 중에 현재 보다 바로 큰 실수, 일 때는 를 반환
참고
nextafter와 동일한 기능을 하지만, y인자를 long double로만 받는 nexttoward라는 함수도 있다. 표현할 수 있는 충분히 큰 Finite한 값이 x일 때, 반환 값은 Infinite이거나 표현할 수 없을 수도 있다. 이에 따라 Overflow로 인한 Range Error가 발생할 수 있다.
4) nexttoward
함수 원형
float nexttowardf(float x, long double y);
double nexttoward(double x, long double y);
long double nexttowardl(long double x, long double y);
C
복사
함수 인자
기준 값을 의미하는 x, 근사값 산출을 위한 방향이 y를 의미한다.
반환 값
일 때는 실수로 표현할 수 있는 수 중에서 현재 보다 바로 작은 실수, 일 때는 실수로 표현할 수 있는 수 중에 현재 보다 바로 큰 실수, 일 때는 를 반환
참고
표현할 수 있는 충분히 큰 Finite한 값이 x일 때, 반환 값은 Infinite이거나 표현할 수 없을 수도 있다. 이에 따라 Overflow로 인한 Range Error가 발생할 수 있다.
8. Minimum, Maximum, Difference Functions
1) fdim
함수 원형
float fdimf(float x, float y);
double fdim(double x, double y);
long double fdiml(long double x, long double y);
C
복사
함수 인자
차이 값 계산을 위한 두 인자 x, y를 받는다.
반환 값
라면 를 반환, 라면 0을 반환 (즉, 와 의 차이를 음수가 아닌 수로 반환)
2) fmax
함수 원형
float fmaxf(float x, float y);
double fmax(double x, double y);
long double fmaxl(long double x, long double y);
C
복사
함수 인자
비교할 두 인자 x, y를 받는다.
반환 값
두 인자 x, y 중 더 큰 인자를 반환
참고
한 인자가 NaN이라면, 나머지 인자를 반환한다.
3) fmin
함수 원형
float fminf(float x, float y);
double fmin(double x, double y);
long double fminl(long double x, long double y);
C
복사
함수 인자
비교할 두 인자 x, y를 받는다.
반환 값
두 인자 x, y 중 더 작은 인자를 반환
참고
한 인자가 NaN이라면, 나머지 인자를 반환한다.
9. Other Functions
1) fabs
함수 원형
float fabsf(float x);
double fabs(double x);
long double fabsl(long double x);
C
복사
함수 인자
어떤 실수도 인자가 될 수 있다.
반환 값
인자로 받은 x의 절대값을 반환
2) abs
abs는 <math.h>에 존재하는 함수가 아니다. 적어도 C 언어에서는 그렇다. C 언어에서의 abs 함수는 <stdlib.h>에 존재하며, int 타입의 인자를 받아 int 타입으로 반환하는 함수이다. abs라는 함수가 <math.h>의 함수가 아님에도 헷갈리는 이유는 그 용도가 라이브러리 이름과의 관련성이 크기 때문이고, C++에서 <cmath>로부터 abs에 대한 다양한 오버로딩 함수를 제공받기 때문이다. C 언어에서 abs 함수를 활용하고 싶다면 위에서 제시된 fabs 함수를 이용하면 된다.
3) fma
함수 원형
float fmaf(float x, float y, float z);
double fma(double x, double y, double z);
long double fmal(long double x, long double y, long double z);
C
복사
함수 인자
x, y는 곱에 사용될 인자이고, z는 덧셈에 사용될 인자이다.
반환 값
인자로 받은 x, y, z에 대해 값을 반환
참고
아래에 주어진 매크로 상수들은 Implementation-Defined Behavior이다. 에 대한 산술 연산보다 더 높은 효율성을 내기 위해 사용된다. (하드웨어 단계의 Multiply-Add Instruction 등이 사용될 때처럼)
FP_FAST_FMA - double 타입의 인자에 대해 만큼 혹은 그 이상으로 빠르게 연산한다.
FP_FAST_FMAF - float 타입의 인자에 대해 만큼 혹은 그 이상으로 빠르게 연산한다.
FP_FAST_FMAL - long double 타입의 인자에 대해 만큼 혹은 그 이상으로 빠르게 연산한다.